Welcome to the Pulse Dispersion Analyzer

About the Quantitative Calculator

This quantitative calculator allows for precise analysis of ultrashort laser pulses by defining spectral properties (analytically or via file import) and observing the impact of spectral phase (GDD, TOD) on the temporal pulse shape, duration, and other characteristics.

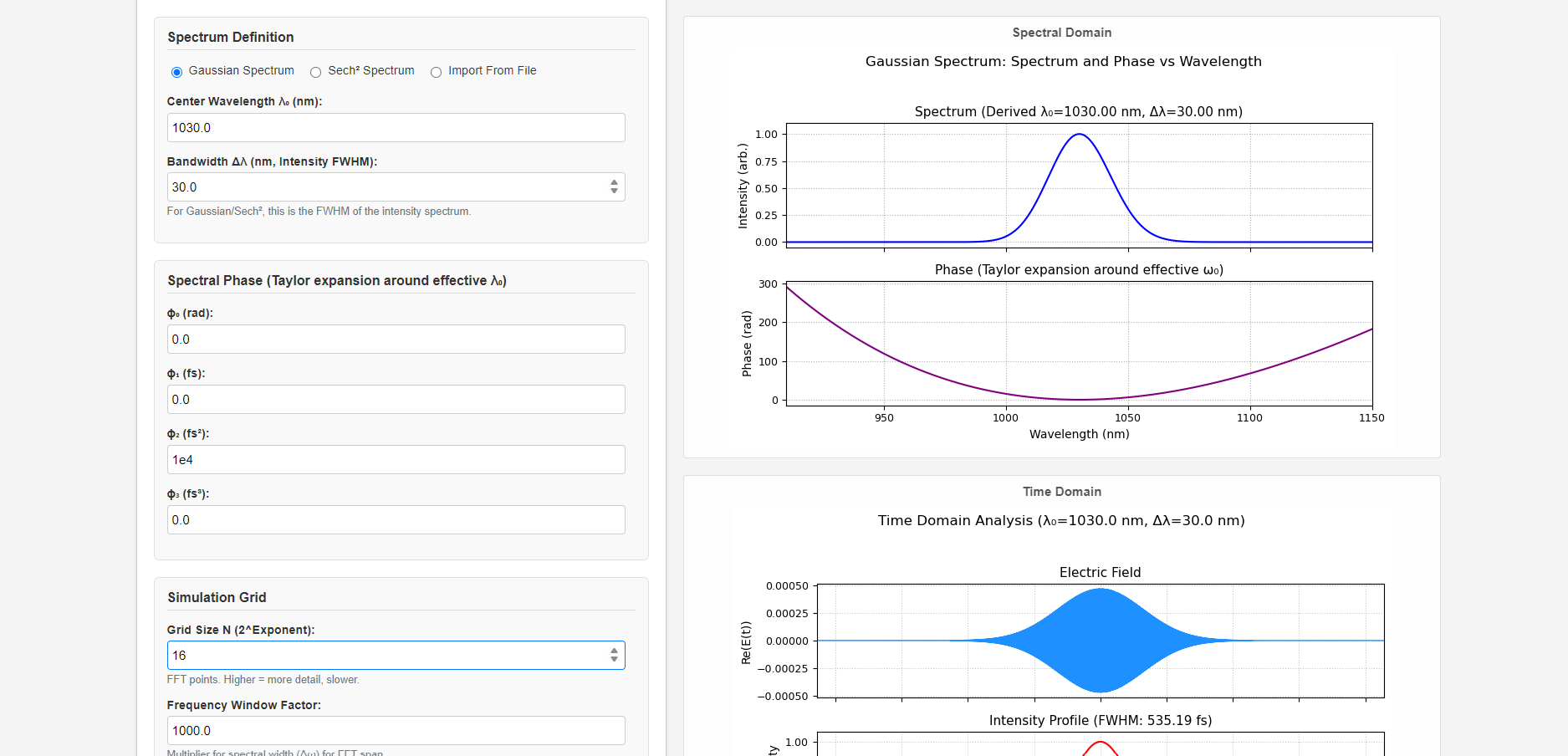
The behavior of an ultrashort pulse is fundamentally governed by the Fourier relationship between its temporal and spectral representations. The temporal electric field, $E(t)$, can be determined from its spectral counterpart, $E(\omega)$, which is characterized by a spectral amplitude $A(\omega)$ and a spectral phase $\Phi(\omega)$.

This calculator focuses on the impact of the spectral phase, which is often described by a Taylor series expansion around the central angular frequency $\omega_0$ (derived from the input central wavelength $\lambda_0$):

$\Phi(\omega) = \phi_0 + \phi_1(\omega-\omega_0) + \frac{1}{2} \phi_2(\omega-\omega_0)^2 + \frac{1}{6} \phi_3(\omega-\omega_0)^3 + \dots$

The coefficients in this expansion have direct physical interpretations:

• $\phi_0$: A constant phase offset.
• $\phi_1$: The group delay, affecting the pulse's arrival time.
• $\phi_2$: The Group Delay Dispersion (GDD), responsible for linear frequency chirp and temporal broadening or compression of the pulse.
• $\phi_3$: The Third-Order Dispersion (TOD), which can introduce pulse asymmetry and satellite pulses.

By adjusting these coefficients, users can directly observe their effects on the pulse's temporal shape, duration, and other properties. The calculations involve Fast Fourier Transforms (FFT) to switch between the spectral and temporal domains.

• Flexible Spectrum Input: Gaussian, Sech², or imported data (CSV/TXT).
• Precise Phase Control: Adjust $\phi_0, \phi_1, \text{GDD}, \text{TOD}$.
• Comprehensive Outputs: Spectral, temporal, and autocorrelation plots.
• Quantitative Analysis: Calculates FWHM for pulse and autocorrelation.
• Simulation Grid Control: Adjustable FFT grid size and frequency window.

Please note this python webapp runs on a paid server with limited resources, thus the grid size cannot exceed 2^22 points. For unlimited grid size, please download the source code and run it locally on your machine.

Launch the calculator using the button above.